
since 2006
Help Sitemap
The correspondence principle connects the quantum mechanics with the classical mechanics, the relativistic classical mechanics with the Newtonian mechanics, and the theory of general relativity with the theory of special relativity.
These examples give us a scenario of constructing a new theory in the grammatical way.
That is to say,
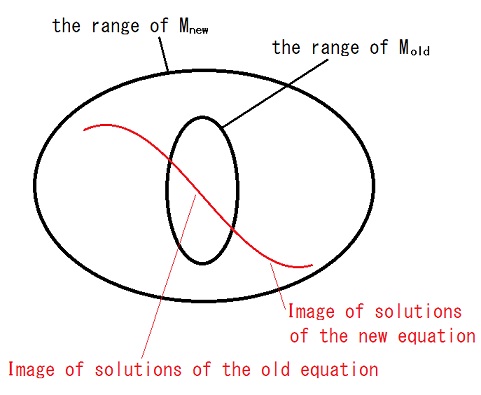
first we propose a new coordinate system Mnew
whose range includes the range of the old coordinate system Mold
as a subset,
and then we seek the equation for Φ(∈the domain of definition of Mnew)
which reduces to the old theory's equation for Ψ(∈the domain of definition of Mold)
when Mnew(Φ) = Mold(Ψ),
and we adopt it as the equation of the new theory.
It reminds me of analytic continuation and Tayler expansion.
However, even when such an equation doesn't exist,
it does not mean immediately that the new grammar has failed,
and we can hope that we find an appropriate equation
which is as near to that as possible.
Actually, in the case of the transition from the classical mechanics
to the existing quantum mechanics,
the Schrödinger equation doesn't have more desirable features
than the Ehrenfest theorem.
This is not a fault of the Schrödinger equation
but a fault of the condition proposed above by me.
An example of making new equation is seen in Uda Equation @ Theory of Quantum History Entangled in Time-like Direction @ Products.
---
The content of this article was presented at APS+JPS 2006 Autumn Meeting.
---
ref. Correspondence principle - Wikipedia