
since 2006
Help Sitemap
Why measurement process is non-deterministic though the time development of quantum state of any system is deterministic if it follows the Schrodinger equation?
I think the following five possibilities as the answer to this question.
(A) Spontaneous breaking of deterministicity.
(B) Entanglement of a quantum history in time-like direction makes correlation between measurement results at different moments.
(C) Quantum history that is superposition of all possible time developments is the solution of Uda equation.
(D) Composite system of the measurement apparatus and the system to be measured is influenced by others.
(E) Macro system does not obey the Schrodinger equation.
(A), (B) and (C) are my original ideas.
Perhaps (D) is the possibility known as the theory of decoherence.
I think of the theory of decoherence as a subspecies of the hidden variable theory and so I think that it does not hit the truth.
Possibly I heard that Shrodinger proposed the cat problem to claim (E).
However I think that macro systems also obey the Schrodinger equation by seeing that specific heat of a macro object in solid state and extremely low temperature coincides with the result of calculation using quantum mechanics.
I thought out (A) by remembering spontaneous breaking of symmetry as a hint.
In dynamical breaking of symmetry, every result appears at equal probability, because symmetry means that any result is not superior than every other result.
Then for long I had incorrectly understood that spontaneous breaking of deterministicity occurs only in breaking of symmetry.
I had incorrectly thought that symmetry makes breaking as nature must select some result among equally superior results.
I had incorrectly thought that nature must select the most superior result deterministically if the condition is not symmetric.
However please consider the case that rigid balls of different radiuses whose centers are on a same line touch each other and are pushed from both ends.
In this case, some ball will slip out of this row and the probability that some ball slips out is different from the probabilities that other balls slip out.
This is an example of how deterministic rule non-deterministically yields various results at different probabilities.
This example means that deterministicity breaks even when the condition is not symmetric.
The ball row is a parable of a wave function in quantum mechanics and pushing here is a parable of measuring and the position where slipping out occurs is a parable of a result of measurement.
You might think that any ball does not slip out.
You might think that some ball slips out or some balls slip out only when the center of some ball are not exactly on the axis or at least one of the pushing forces is not exactly on the axis.
By the following example, I explain that it is not so.
In constant uniform gravitational field and the Newtonian equation of motion, a massive point particle constrained on the curved line defined by the following condition can move to right side and can move to left side and can keep staying if x = y = z = 0 and dx/dt = dy/dt = dz/dt = 0 when t = 0.
Condition: z = 0 and d|x|/dy = √(y-1/3 - 1) and (x, y, z) = (0, 0, 0) is the top of the line and y-axis has the same direction as the direction of gravity.
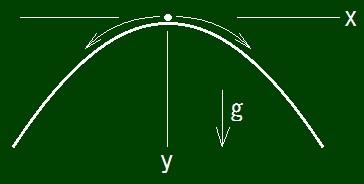
Here (x, y, z) represents the position of the particle and a point on the curved line, and t represents a time.
The Newtonian equation of motion can not determine which of three motions realizes.
You can understand it by calculating time of climbing up, which equals the time of slipping down, and confirming that it is finite.
More exactly saying, the particle can continue to stay till an arbitrary moment and then start slipping down.
By conservation of energy, mgy = (m/2)[(dx/dt)2 + (dy/dt)2] = (m/2)(dy/dt)2[(dx/dy)2 + 1].
∴ (dy/dt)2 = 2gy/[(dx/dy)2 + 1] = 2gy/[(y-1/3 - 1) + 1] = 2gy/y-1/3 = 2gy4/3.
∴ dt/dy = [1/√(2g)]y-2/3.
∴ ∫0Y dy dt/dy = [3/√(2g)]Y1/3.
This is the time for the value of y of the particle to vary from 0 to Y, and it has been proved finite.
Here g is the gravitational acceleration and m is the mass of the particle.
Please correct dimensionality appropriately.
Exactly saying, it is not that deterministic rule makes non-deterministic process, the Newtonian equation is not perfectly deterministic, it must be complemented by some probabilistic rule.
For the above reasons, we must understand that (A) is independent of (D).
It is disadvantageous for (A) that the Schrodinger equation is different from the Newtonian equation of motion at the following point.
The Schrodinger equation includes only the first derivative with respect to time while the Newtonian equation includes the second derivative with respect to time.
In the context of (B), how measurement process goes and what measurement is are not asked and are not answered.
It may be correct to interpret Feynman's path integral as (B) and its integrand as a quantum history.
However integration is not taken before the first measurement and after the second measurement in Feynman's path integral while (B) looks different from it.
Moreover Feynman's path integral is applied only to measurements done two times while (B) is applied to measurements done arbitrarily many times.
I made the stacked daruma game formula to prove (B) true and failed.
I found an important mistake in the stacked daruma game formula.
Let x be the degree of freedom of a system to be measured and let y be the degree of freedom of the measurement apparatus and let Ψ(x, y; t) be a time-dependent wave-function of the composite system of those systems in the old quantum grammar and let measurement be done at t = 0.
Then (C) is the following idea.
Ψ(x, y; t) = ξ(x)η(y) when t < 0.
Ψ(x, y; t) = ξ1(x)η1(y) or Ψ(x, y; t) = ξ2(x)η2(y) when t > 0.
Ψ1(x, y; t) = ξ(x)η(y) when t < 0.
Ψ1(x, y; t) = ξ1(x)η1(y) when t > 0.
Ψ2(x, y; t) = ξ(x)η(y) when t < 0.
Ψ2(x, y; t) = ξ2(x)η2(y) when t > 0.
exp φ1(x, y; t) ≡ Ψ1(x, y; t) for any t.
exp φ2(x, y; t) ≡ Ψ2(x, y; t) for any t.
Φ1[X, Y] ≡ exp[α∫dt φ1(X(t), Y(t); t)].
Φ2[X, Y] ≡ exp[α∫dt φ2(X(t), Y(t); t)].
Φ1 + Φ2 is a solution of the Uda equation though neither Φ1 nor Φ2 is a solution of the Uda equation.
By the way, the decoherence theory supposes that the Schrodinger equation says that Ψ(x, y; t) = ξ1(x)η1(y) + ξ2(x)η2(y) after measurement.
(C) opposes the thought that measurement is such a process.
(C) may give a mathematical expression to the many-worlds interpretation.
If it does so, many-worlds interpretation will be raised from an interpretation to a theory.
(D) is the following idea.
Let x be the degree of freedom of a system to be measured and let y be the degree of freedom of the measurement apparatus and let z be the degree of freedom of all other existences and let Ψ(x, y, z; t) be a time-dependent wave-function of the composite system of those systems in the old quantum grammar and let measurement be done at t = 0.
Ψ(x, y, z; t) = ξ(x)η(y)ζ(z) when t < 0.
Ψ(x, y, z; t) = [Σiξi(x)ηi(y)]ζ(z) when t = ε> 0.
∃i; ∃φ; Ψ(x, y, z; t) = ξi(x)φ(y, z) when t > δ>ε.
Ψ obeys the Schrodinger equation.
Because of taking z into account for rigor, quantum state ζ of all exterior existences is not known more than probabilistically, and so measurement result ξi looks like appearing probabilistically.
This is perhaps a paraphrase of the theory of decoherence and is a kind of the hidden variable theory.
In the theory of decoherence, influence of z perhaps is replaced by some phenomenological potential and Ψ(x, y; t) is thought to obey the Schrodinger equation with the potential.
In it, k such that entangled state Σiξi(x)ηi(y) breaks to an unentangled state ξk(x)ηk(y) after t = ε till t = δ is thought to exist.
I think that such an idea has the following shortcoming.
Actually the probability that ξi results depends only on ξ while (D) says that the probability depends on both ξ and the probability distribution of ζ.
Moreover (D) also says that the probability depends on how z interact with x and y.
It is not sufficient only to show that some phenomenological potential realizes the needed decoherence.
In addition to it, it is also necessary to derive such a phenomenological potential from a concrete interaction between (x, y) and z.
If it is proved that any set of a probability distribution of ζ and an interaction between (x, y) and z can not produce such a phenomenological potential, (D) must be abandoned.
---
The content of this page will be presented at JPS 2018 Spring Meeting.