
since 2006
Help Sitemap
In this page, I make Stacked Daruma Game Formula by using Exact Solution of Uda Equation (5).
Stacked Daruma Formula gives transition amplitude.
First I chose a quantum history represented by functional Φ such that
Φ[ν] = ∑k exp{α∫-∞∞dt[-iωtν(t) + a(k)ν(t) + ib(k)ν(t)]}
where a(k)n and b(k)n are defined as follows.
|uk> = ∑n=0∞ λ(k)n|n> = ∑n=0∞ exp(a(k)n + ib(k)n)|n>.
{ |uk> | ∃k } is a orthonotmal basis of the state space.
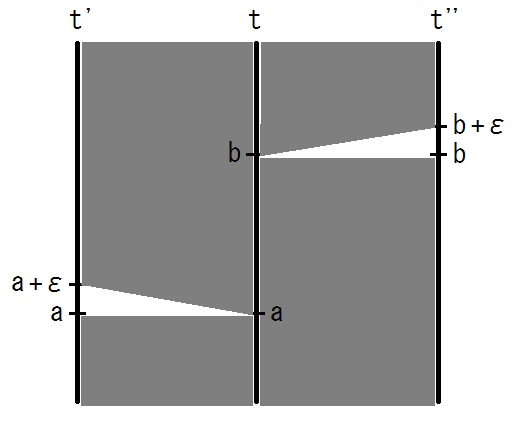
| ν'(t') = ν(t') if t' < a. ν'(t') = ν(a) if a ≦ t' < a + ε. ν'(t') = ν(t' - ε) if t' ≧ a + ε. ν''(t'') = ν(t'') if t'' < b. ν''(t'') = ν(b) if b ≦ t'' < b + ε. ν''(t'') = ν(t'' - ε) if t'' ≧ b + ε. |
 |
ε = 1/α, b - a = Nε,
ν(t) = nk if a + kε ≦ t < a + (k + 1)ε.
 .
.Φ[ν''] = ∑k exp{α∫-∞bdt''[-iωt''ν''(t'') + a(k)ν''(t'') + ib(k)ν''(t'')]
+ α∫bb+εdt''[-iωt''ν''(t'') + a(k)ν''(t'') + ib(k)ν''(t'')]
+ α∫b+ε∞dt''[-iωt''ν''(t'') + a(k)ν''(t'') + ib(k)ν''(t'')]}
= ∑k exp{α∫-∞bdt''[-iωt''ν(t'') + a(k)ν(t'') + ib(k)ν(t'')]
+ α∫bb+εdt''[-iωt''ν(b) + a(k)ν(b) + ib(k)ν(b)]
+ α∫b+ε∞dt''[-iωt''ν(t'' - ε) + a(k)ν(t''-ε) + ib(k)ν(t''-ε)]}
= ∑k exp{αε[-iω(b + ε/2)ν(b) + a(k)ν(b) + ib(k)ν(b)]}
× exp{α∫-∞bdt[-iωtν(t) + a(k)ν(t) + ib(k)ν(t)] + α∫b∞dt[-iω(t + ε)ν(t) + a(k)ν(t) + ib(k)ν(t)]}
= ∑k ψk(ν(b), b + ε/2) exp{α∫-∞∞dt[-iωtν(t) + a(k)ν(t) + ib(k)ν(t)] - iωεα∫b∞dt ν(t)}.
Φ[ν']* = ∑j ψj(ν(a), a + ε/2)* exp{α∫-∞∞dt[iωtν(t) + a(j)ν(t) - ib(j)ν(t)] + iωεα∫a∞dt ν(t)}.
Φ[ν''] Φ[ν']* = ∑k ∑j ψk(ν(b), b + ε/2)ψj(ν(a), a + ε/2)*
× exp{α∫-∞∞dt[a(k)ν(t) + ib(k)ν(t)] exp{α∫-∞∞dt[a(j)ν(t) - ib(j)ν(t)]
× exp[iωεα∫abdt ν(t)]
= ∑k ∑j ψk(ν(b), b + ε/2)ψj(ν(a), a + ε/2)* [Πs=-∞∞ λ(k)n(s) λ(j)n(s)*] exp[(i/
<ν(b), ν(a)>Daruma = ∑k ∑j ψk(ν(b), b + ε/2)ψj(ν(a), a + ε/2)* (δjk)∞
= ∑k ψk(ν(b), b + ε/2)ψk(ν(a), a + ε/2)* ∵ (δjk)∞ = δjk
= ∑k <ν(b)|exp[-(i/
= <ν(b)| exp[-(i/
= <ν(b)| exp[-(i/
= exp[-(i/
= exp[-iω(b - a)ν(a)]δν(b)ν(a).
Perhaps Daruma contraction can be defined as
<χ(b), χ(a)>Daruma = ∑ν(b)=0∞ ∑ν(a)=0∞ <vχ(b)|ν(b)><ν(b), ν(a)>Daruma<ν(a)|vχ(a)>
= ∑ν(b)=0∞ ∑ν(a)=0∞ <vχ(b)|ν(b)><ν(b)| exp[-(i/
= <vχ(b)| exp[-(i/
where |vx> is an eigenvector of the position operator with eigenvalue x.
For example, if we take ε = 1/(2α),
[Πk=-∞∞∑n(k)=0∞] Πs=-∞∞ [λ(k)n(s)]1/2 [λ(j)n(s)*]1/2
arises as a factor in the calculation.
However, ∑n=0∞ [λ(k)n]1/2 [λ(j)n*]1/2 is not concerned with ∑n=0∞λ(k)n λ(j)n* = δjk at all.
So, ε ≠ 1/α is impossible.
Especially ε → +0 is impossible because ∑n=0∞ [λ(k)n]αε [λ(j)n*]αε → ∑n=0∞ 1 = ∞ as ε → +0.
If λ(k)n = δkn and ε → +0,
∑n=0∞ [λ(k)n]αε [λ(j)n*]αε = ∑n=0∞ δknδjn = δjk,
exp{αε[-iω(b + ε/2)ν(b) + a(k)ν(b) + ib(k)ν(b)]} = [ψk(ν(b), b + ε/2)]αε = δν(b)kexp[-ikωαε(b + ε/2)] → δν(b)k,
<ν(b), ν(a)>Daruma = ∑k ∑j δν(b)kδν(a)j(δjk)∞
= ∑k δν(b)kδν(a)k
= δν(b)ν(a)
= <ν(b)|ν(a)>.
This result also is undesirable because it does not represent time development at all.
Can <ν(b), ν(a)>Daruma be modified as
<ν(b), ν(a)>Daruma = [Πk=-∞∞∑n(k)=0∞]exp[-(i/
and ε → +0 ?
Such a modification is also impossible because Φ[ν] consists of many terms.
Each term of Φ[ν''] Φ[ν']* is not raised to the αε-th power.
If λ(k)n = δkn and ε → +0 and
<ν(b), ν(a)>Daruma = {[Πk=-∞∞∑n(k)=0∞]exp[-(i/
<ν(b), ν(a)>Daruma = δν(b)ν(a)exp[-iω(b - a)ν(a)] = <ν(b)| exp[-(i/
This might be another candidate but I feel that this too is not very plausible because of λ(k)n = δkn and
exp[-(i/
First assumption in this page can be criticized for being arbitrary.
So, now I rechose a quantum history represented by functional Φ such that
Φ[ν] = ∑r ∑k exp{α∫-∞∞dt[-iωtν(t) + a(r, k)ν(t) + ib(r, k)ν(t)]}
where a(r, k)n and b(r, k)n are defined as follows.
|u(r)k> = ∑n=0∞ λ(r, k)n|n> = ∑n=0∞ exp(a(r, k)n + ib(r, k)n)|n>.
Br ≡ { |u(r)k> | ∃k } is an orthonotmal basis of the state space for each r.
∀r; ∀k; ∀s; r ≠ s ⇒ not[∃j; ∃c ∈ C; |u(r)k> = c|u(s)j>].
∑n=0∞ λ(r, k)n λ(s, j)n* = ∑n=0∞ <n|u(r)k> <u(s)j|n> = <u(s)j|u(r)k>.
r ≠ s ⇒ ∀j; ∀k; | <u(s)j|u(r)k> | < 1.
∴ [∑n=0∞ λ(r, k)n λ(s, j)n*]∞ = δrsδjk.
<ν(b), ν(a)>Daruma = (∑r 1) × <ν(b)| exp[-(i/
---
The content of this page was developed in Number Representation of Uda Equation @ Quantum History Theory @ Problems.