
since 2006
Help Sitemap
I noticed that it is too difficult to derive a solution for a specific potential and that I should derive a potential for a specific solution.
At first, I replace ∫-∞∞dt V(χ(t)) by a general real valued functional V[χ] in the Uda equation.

In this page, I investigate how a potential functional V is for a solution functional Φ of the following specific form.
Then the Uda equation reduces to the following condition to be obeyed by function Δ.
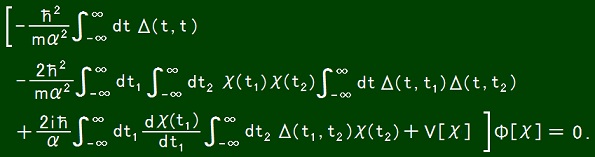
V[χ] is real and so Δ(t1, t2) has to be pure imaginary and Δ(t, t) has to be real.
Therefore Δ(t, t) has to be 0 whatever the value of t is.
That Δ(t1, t2) = iδ'(|t2 - t1|) leads to failure.
The following possibility leads to a consistent result.
Δ(t1, t2) = i f(t1 + t2)[δ(t2 - t1 -ε) + δ(t1 - t2 -ε)].
f is a real valued function.
ε> 0.
It is as follows.
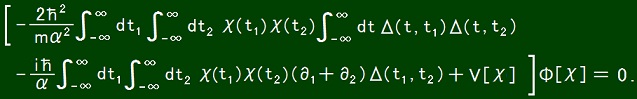
Δ(t, t1) Δ(t, t2)
= - f(t + t1) f(t + t2)[δ(t1 - t -ε) + δ(t - t1 -ε)][δ(t2 - t -ε) + δ(t - t2 -ε)]
= - f(t + t1) f(t + t2)[δ(t1 - t -ε)δ(t2 - t -ε) + δ(t1 - t -ε)δ(t - t2 -ε)
+ δ(t - t1 -ε)δ(t2 - t -ε) + δ(t - t1 -ε)δ(t - t2 -ε)]
= - [f(t1 + t2 - ε)]2δ(t1 - t -ε)δ(t2 - t -ε)
- f(t1 + t2 + ε)f(t1 + t2 - ε)[δ(t1 - t -ε)δ(t - t2 -ε) + δ(t - t1 -ε)δ(t2 - t -ε)]
- [f(t1 + t2 + ε)]2δ(t - t1 -ε)δ(t - t2 -ε)].

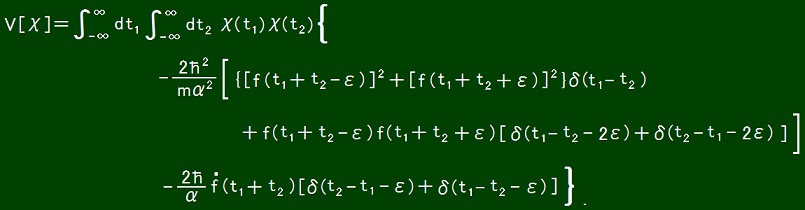
Though ε is forbidden to be zero, as ε→ 0,

If f(τ) = c(an arbitrary constant independent of τ), this solution can not realize a positive valued V.
If f(τ) = c tan(-κτ), it follows that

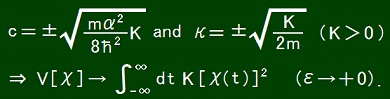
This solution is not perfect because tan(-κτ) diverges at τ = (π/2 + nπ)/κ.
Then let us chose f as follows.
f(τ) = c tan[-κ(τ- ak)] when bk ≦ τ < bk+1.
・・・ < b-2 < b-1 < b0 < b1 < b2 < ・・・.
bk < ak < bk+1.
ak - bk <π/2 and bk+1 - ak <π/2.
For such a function f, it follows that
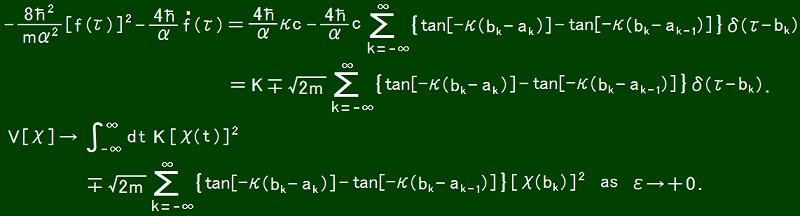
This potential means that an impulsive force works at each t = bk.
Φ is interpreted as meaning that the wavelength and the degree of locality vibrate and are reset by the impulsive force.
This result makes sense but is not newer than the result of pre-Uda quantum mechanics.
I also investigated what happens if f(τ) = c tanh(κτ).
The result is as follows.
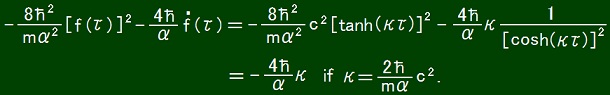
This solution can not realize a positive valued V.
As an another case, if f(τ) = -κτ, it follows that
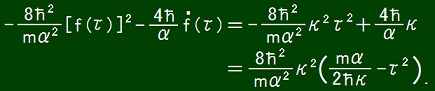
In this solution, V is positive as far as τ2 < mα/(2
For letting (4
Then mα/(2
2/ω is too short as a time for saying that V is the potential of a harmonic oscillator.
The wave function ψ(x) of a harmonic oscillator in pre-Uda quantum mechanics consists of exp(-kx2) where k is real.
The difference between it and pure imaginarity of above Δ(t1, t2) seems to strongly prevent my making a solution of Uda equation for positive V.
If (∂1+∂2)Δ(t1, t2) = 0, Δ(t1, t2) does not have to be pure imaginary, it is allowed to be real.
However even if so, Δ(t, t) must be zero for avoiding divergence.
Then let us consider the case characterized by Δ defined by the following condition.
Δ(t1, t2) = A[δ(t2 - t1 -ε) + δ(t1 - t2 -ε)]
where A is a real number.
For this Δ, the Uda equation reduces to the following equation.

As follows, this equation leads to how V is.
Δ(t, t1)Δ(t, t2) = A2[δ(t1 - t -ε)δ(t2 - t -ε) + δ(t1 - t -ε)δ(t - t2 -ε) + δ(t - t1 -ε)δ(t2 - t -ε) + δ(t - t1 -ε)δ(t - t2 -ε)].
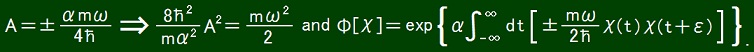
That the integrand of Φ[χ] can be positive is different from pre-Uda quantum mechanics.
However it is not a difference from pre-Uda Schrodinger equation.
In pre-Uda quantum mechanics, positive variable of exp was rejected not because it contradicts to Schrodinger equation but because it is not physical.
So we can say that the above result well coincides with pre-Uda quantum mechanics.
In the meaning that ε = 0 is forbidden, Uda equation restrict how potential is.
Although it has not been proved yet, it seems to be impossible to write V[χ] = ∫-∞∞dt F(χ(t)) using some function F.
While a wave-function of a stationary state also is formally time-dependent in pre-Uda quantum mechanics, Uda equation claims that it is not so.
I expect that Uda equation will bring some new physics via this difference.
At the same time, I am afraid that this difference will kill Uda equation.
As an example, below I describe the physics of the solution defined by the following Δ.
Δ(t1, t2) = -A(t1 - t2)2exp[-B(t1 - t2)2] where A > 0 and B > 0.
Because
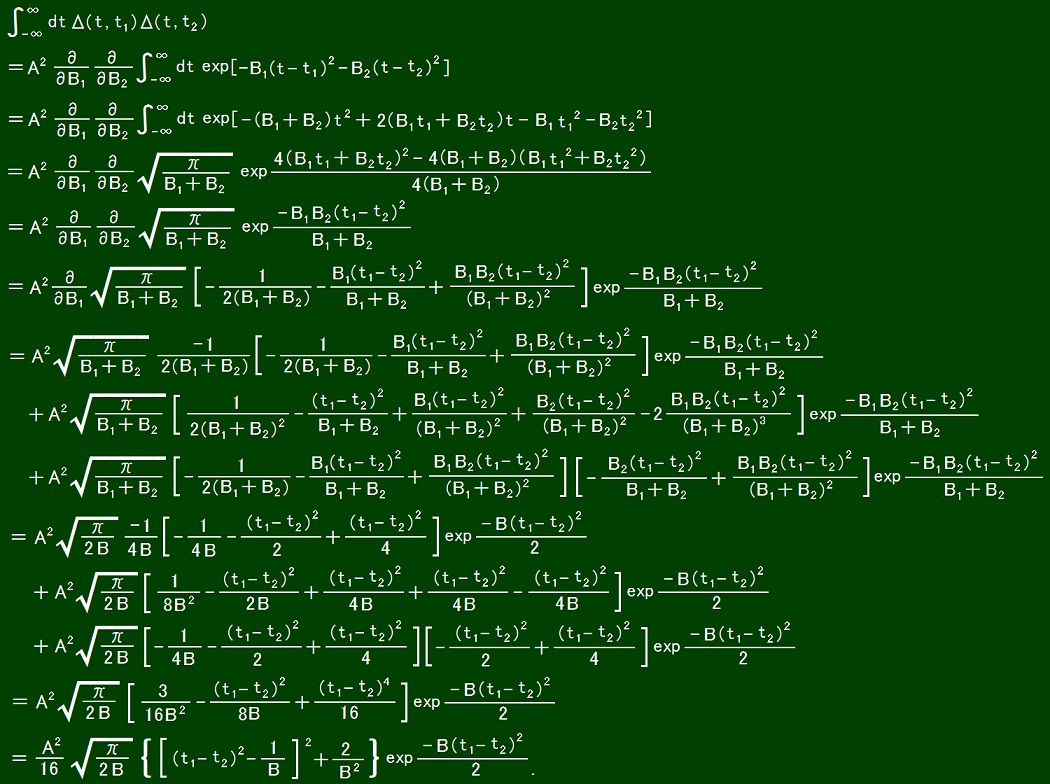
In the above calculation, the following substitutions were done after differentiations.
B1 = B, B2 = B.
The potential with which Uda equation has the above solution is the following functional.
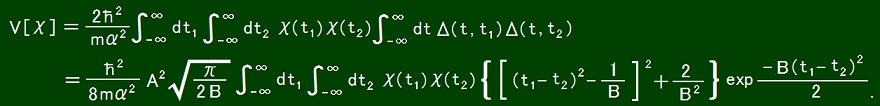
When the action is as
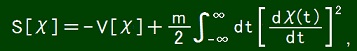
the classical equation of motion defined as δS[χ]/δχ(t) = 0 is as follows.
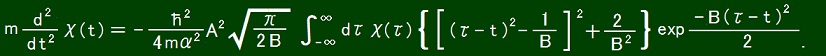
From the aspect of causality, I wonder if it should hold that
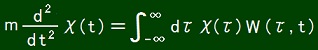
where W(τ, t) = 0 if τ > t.
However, the principle of least action only mentions how a history is as a whole, and it does not claim that present and future part of history must be determined by past part of history.
Moreover, why must we think of force as cause, why must we think of acceleration as result?
We can recover the ordinary causality by rewriting my equation as follows.
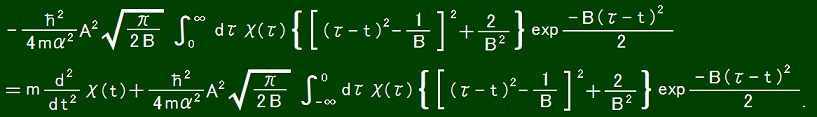
This equation describes how total past force and present acceleration determine total future force.
Here, not only past force but also present acceleration is thought of as cause, and future force is thought of as result.
The total past force is like incoming money.
The present acceleration is like outgoing money.
The total future force is like a debt.
In my equation, the earlier the income is, the less it contributes to present acceleration.
It does not resemble to money.
However, the later paying back of debt is, the more it is.
This resembles to money.
If we think so, the causality is recovered even in my equation.
However we can say in any way if only in words.