Exact Solution of Uda Equation (1) @ Quantum History Theory @ Products @ Forum @ www.GrammaticalPhysics.ac

since 2006
Help　Sitemap

< Forum >

< Products >

< Quantum History Theory >

< Exact Solution of Uda Equation (1) >

On 2015/12/18, I discovered that the Uda equation has the following solution when V =0.
　

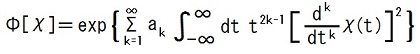
where a_k is determined by some appropriate condition.

I will prove it below.

　

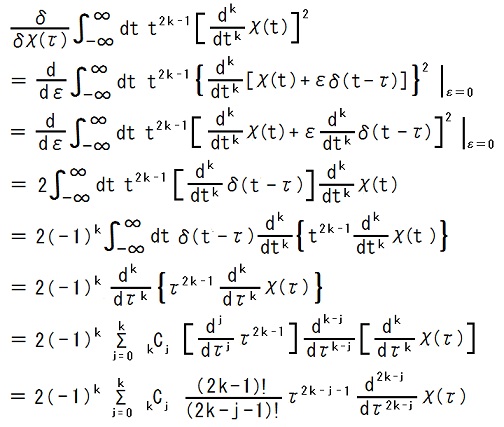
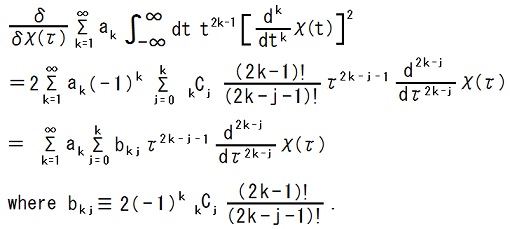
		j
		0	1	2	3	4	5	6	・・・
k	1	2k-j =2	2k-j =1
	2	2k-j =4	2k-j =3	2k-j =2
	3	2k-j =6	2k-j =5	2k-j =4	2k-j =3
	4	2k-j =8	2k-j =7	2k-j =6	2k-j =5	2k-j =4
	5	2k-j =10	2k-j =9	2k-j =8	2k-j =7	2k-j =6	2k-j =5
	6	2k-j =12	2k-j =11	2k-j =10	2k-j =9	2k-j =8	2k-j =7	2k-j =6
	・・・	・・・	・・・	・・・	・・・	・・・	・・・	・・・	・　　・　　　　・

2k-j = 2s-1 (s∈N)	(k, j) = (s, 1), (s + 1, 3), (s + 2, 5), ・・・, (2s - 1, 2s - 1)	s ≦ k ≦ 2s - 1 j = 2(k - s) + 1
2k-j = 2s (s∈N)	(k, j) = (s, 0), (s + 1, 2), (s + 2, 4), ・・・, (2s, 2s)	s ≦ k ≦ 2s j = 2(k - s)

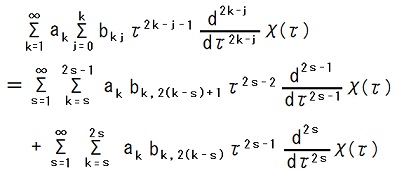
I want to adjust the value of a_k such that all terms other than the term of 2k - j = 1 vanishes.

Σ_k=s^2s-1 a_k b_{k, 2(k-s)+1} = 0 (s≧2)
Σ_k=s^2s a_k b_{k, 2(k-s)} = 0 (s∈N)

∴ a_2s-1 = -(1/b_{2s-1, 2s-1})Σ_k=s^2s-2 a_k b_{k, 2(k-s)+1} (s≧2)
　　a_2s = -(1/b_{2s, 2s})Σ_k=s^2s-1 a_k b_{k, 2(k-s)} (s∈N)

a₂ = -(1/b₂₂)a₁b₁₀
　= (1/6)a₁ ∵ b₂₂ = 12, b₁₀ = -2,
a₃ = -(1/b₃₃)a₂b₂₁
　= (1/10)a₂ ∵ b₃₃ = -120, b₂₁ = 12
　= (1/60)a₁,
and so on.

After the adjustment, the following condition holds.
　

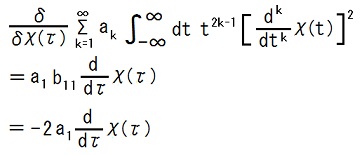
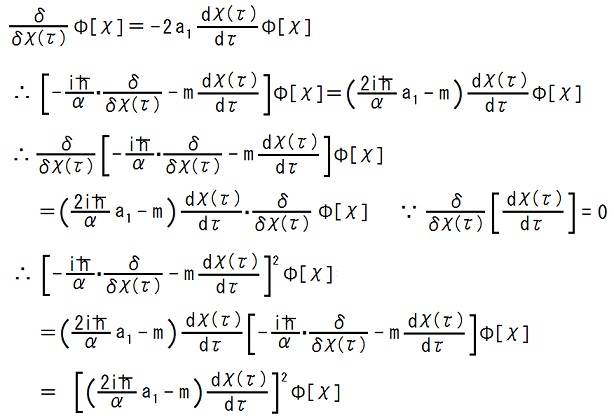
When a₁ = mα/(ih), it holds that
　

.
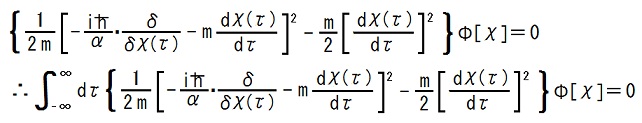This is the same as the reduced form of the Uda equation when V = 0.

a₂ = (1/6)a₁ = mα/(6ih),
a₃ = (1/60)a₁ = mα/(60ih),
and so on.

---
This article is about the problem refered to in 19th @ December 2015 @ News.

Author Yuichi Uda, Write start at 2016/03/26/15:32JST, Last edit at 2016/04/01/17:19JST