
since 2006
Help Sitemap
On 2017/04/05, just before starting sleep, I thought that the Uda equation has the following solution when V =0.

Later, I noticed that the integral diverges when the delta function factor is not zero in the above expression.
Then I improved the above expression to write the following one.
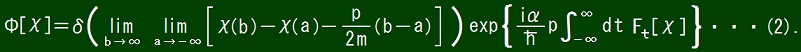
where Ft is a functional defined by the following conditions.
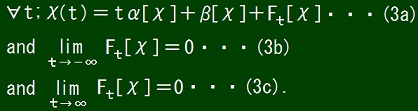
These conditions define α and β and Ft and their domains of definition at the same time.
Each Ft is a functional for any value of t.
To let you understand what I wrote above, I should note down my idea as follows though it makes understanding dependence of α and β and χ'(t) on χ difficult.
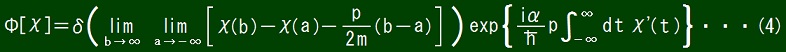
where χ' is a function defined as
∀t; χ(t) = αt + β + χ'(t) ・・・(5a)
for a function χ such that
∃α,β; [χ(t) - (αt + β) tends to 0 as t tends to ±∞] ・・・(5b).
Below I prove that functional Φ defined by expression (2) is a solution of the Uda equation.
There I will use the following properties of the delta function.
δ(τ - t) tends to 0 as τ tends to ∞.
δ(τ - t) tends to 0 as τ tends to -∞.
If all of conditions (3a) and (3b) and (3c) hold, all of following conditions (3a)' and (3b)' and (3c)' hold.
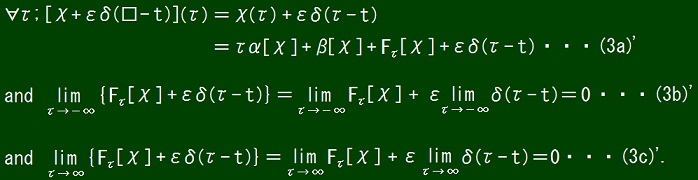
These facts together with the definition of α and β and Fτ mean that
α[χ + εδ(□ - t)] = α[χ] ・・・(6a1)
and β[χ + εδ(□ - t)] = β[χ] ・・・(6a2)
and Fτ[χ + εδ(□ - t)] = Fτ[χ] + εδ(τ - t) ・・・(6a3).
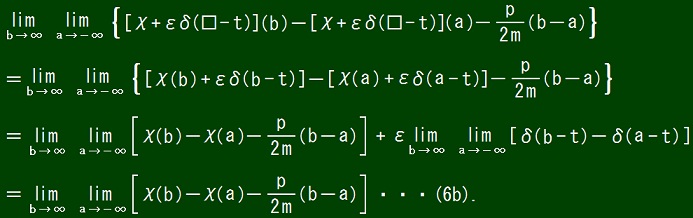
From equations (2) and (6a3) and (6b), it follows that
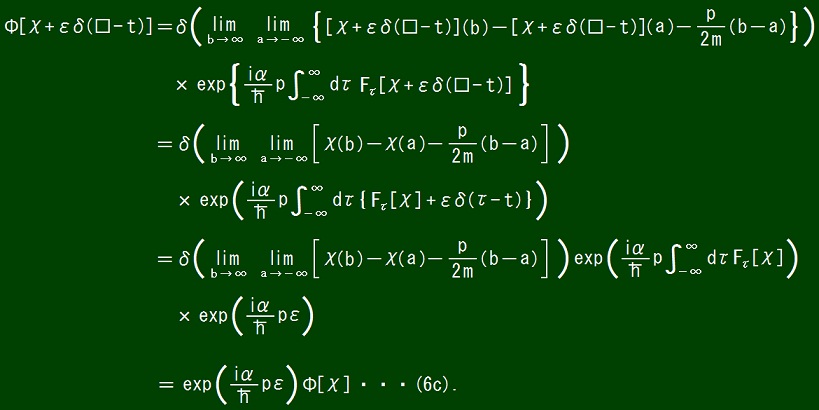
From equation (6c), it follows that
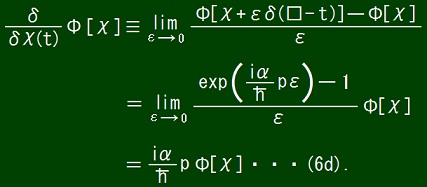
From equation (6d), it follows that
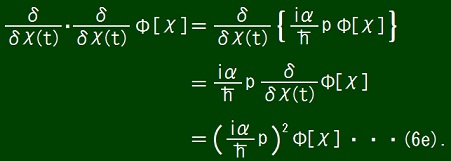
From equations (6d) and (6e), it follows that
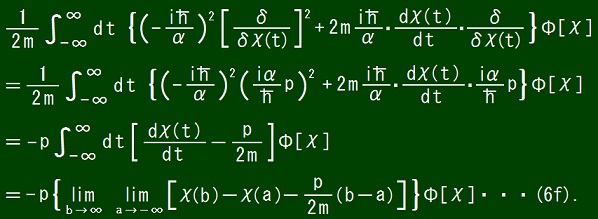
From the property of the delta function, it follows that

From equations (2) and (6f) and (6g), it follows that
Equation (7) is no other than the reduced form of the Uda equation, and so the proof is now completed.
For any function f and any number a, by the notation f(□ - a) I represented a function such that ∀x; [f(□ - a)](x) = f(x - a).
Expression (2) means that Φ[χ] = 0 if
This means that the quantum history represented by functional Φ defined by expression (2) is entangled in time-like direction.
I name this entanglement asymptotically constant velocity entanglement.