since 2006 Help　Sitemap
	< Forum >
		< Products >
			< Quantum History Theory >
				< Uda Equation of Free Dirac Field >
					The content of this page was developed in Uda Equation of Dirac Field @ Quantum History Theory @ Problems. The Hamiltonian: H = ∫d3x ψ†(x)γ0(-ihcγk∂k + mc2)ψ(x). The quantization conditions: [ψα(x), ψ†β(y)]+ = δαβδ3(x - y), [ψα(x), ψβ(y)]+ = 0. The above expressions are of the existing theory. Now I start explaining my theory of quantum history. [ψα(x), ψ†β(y)]+ = δαβδ4(x - y), [ψα(x), ψβ(y)]+ = 0. I assume so by seeing [Z(t), Z†(t')]+ = δ(t - t') and [Z(t), Z(t')]+ = 0 in Uda Equation of Fermionic Mechanics. The left hand side of Uda equation: ih∫-∞∞dt∫d3x Σα=14ψ†α(x, t)(∂/∂t)ψα(x, t) |Φ> 　= ih∫-∞∞d(ct)∫d3x ψ†(x, t)[∂/∂(ct)]ψ(x, t) |Φ> 　= ih∫d4x ψ†(x)(∂/∂x0)ψ(x) |Φ> (∵ x0 = ct) 　= ih∫d4x ψ†(x)∂0ψ(x) |Φ>. I assume so by seeing ih∫-∞∞dt Z†(t)(d/dt)Z(t) |Φ> in Uda Equation of Fermionic Mechanics. The concept is to shift all spacetime points at which there is a particle by -ε in time-like direction. Because (γ0γ0)αβ = δαβ, the left hand side of Uda equation is ∫d4x ψ†(x)γ0(ihγ0∂0)ψ(x) |Φ>. Uda Equation: ∫d4x ψ†(x)γ0(ihγ0∂0)ψ(x) |Φ> = ∫-∞∞dt∫d3x ψ†(x, t)γ0(-ihcγk∂k + mc2)ψ(x, t) |Φ> ∴ ∫d4x ψ†(x)γ0(ihγ0∂0)ψ(x) |Φ> = ∫-∞∞d(ct)∫d3x ψ†(x, t)γ0(-ihγk∂k + mc)ψ(x, t) |Φ> ∴ ∫d4x ψ†(x)γ0(ihγ0∂0)ψ(x) |Φ> = ∫d4x ψ†(x)γ0(-ihγk∂k + mc)ψ(x) |Φ> ∴ ∫d4x ψ†(x)γ0(-ihγμ∂μ + mc)ψ(x) |Φ> = 0. This expression was first published in 15th @ May 2019 @ News at about 2019/05/15/15:00(Japan Standard Time). In case, below I note down details. [ψα(x), ψ†β(y)]+ = ψα(x)[ψβ(y)]† + [ψβ(y)]†ψα(x) 　= δαβδ(x1 - y1)δ(x2 - y2)δ(x3 - y3)δ(x0 - y0). [ψα(x), ψβ(y)]+ = ψα(x)ψβ(y) + ψβ(y)ψα(x) = 0. ∫-∞∞dx1∫-∞∞dx2∫-∞∞dx3∫-∞∞dx0 Σα=14Σβ=14 [ψα(x)]† [-ihΣμ=03(γ0γμ)αβ∂μ + mc(γ0)αβ] ψβ(x) |Φ> = 0. 　 　σ1σ2 = -σ2σ1 = iσ3, σ2σ3 = -σ3σ2 = iσ1, σ3σ1 = -σ1σ3 = iσ2, 　σ1σ1 = σ2σ2 = σ3σ3 = σ0. 　 　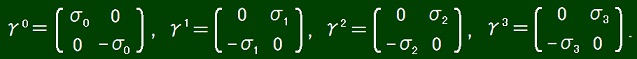( [γμ, γν]+ )αβ = (γμγν + γνγμ)αβ = 2gμνδαβ, 　g00 = 1, g11 = g22 = g33 = -1, 　μ≠ν ⇒ gμν = 0.
				Author Yuichi Uda, Write start at 2019/05/18/15:19JST, Last edit at 2019/05/20/16:46JST