
since 2006
Help Sitemap
The content of this page is toward Uda equation of Free Dirac Field and was developed in Uda Equation of Dirac Field @ Quantum History Theory @ Problems.
In this page, I treat a system of two real degrees x and y of freedom.
I let the Hamiltonian H of this system be as H = a(x2 + y2).
At first, I define a complex variable z as z = x + iy.
Then H = az*z where z* is the complex conjugate of z.
Quantization of this system is done as follows.
X is an Hermitian operator whose eigenvalue is x.
Y is an Hermitian operator whose eigenvalue is y.
Z ≡ X + iY.
[Z, Z]+ ≡ ZZ + ZZ = 0 ∴ Z2 = 0.
[Z, Z†]+ ≡ ZZ† + Z†Z = 1.
H = aZ†Z.
Z2 = 0 ⇔ X2 - Y2 + iXY + iYX = 0 ⇔ [X, Y]+ = i(X2 - Y2).
ZZ† + Z†Z = 1 ⇔ 2X2 + 2Y2 = 1 ⇔ X2 + Y2 = 1/2.
H = aZ†Z = a(X2 + Y2 + iXY - iYX) = a(i[X, Y]- + 1/2).
Z†Z|n> = n|n>, <n|n> = 1, n ∈ R.
n2 = n2(|n>, |n>) = (n|n>, n|n>) = (Z†Z|n>, Z†Z|n>) = <n|Z†ZZ†Z|n> = <n|Z†(1 - Z†Z)Z|n> = <n|Z†Z|n>
∵ Z2 = 0
∴ n2 = n<n|n> = n
∴ n = 0 or 1.
(Z|0>, Z|0>) = <0|Z†Z|0> = 0<0|0> = 0 ∵ Z†Z|0> = 0|0>.
∴ Z|0> = 0.
(Z†|1>, Z†|1>) = <1|ZZ†|1> = <1|(1 - Z†Z)|1> = 0 ∵ Z†Z|1> = |1>.
∴ Z†|1> = 0.
Z†ZZ†|0> = Z†(1 - Z†Z)|0> = Z†|0> ∵ Z|0> = 0.
(Z†|0>, Z†|0>) = <0|ZZ†|0> = <0|(1 - Z†Z)|0> = <0|0> = 1 ∵ Z|0> = 0.
∴ Z†|0> = |1>.
Z†ZZ|1> = 0 = 0Z|1> ∵ Z2 = 0.
(Z|1>, Z|1>) = <1|Z†Z|1> = <1|1> = 1 ∵ Z†Z|1> = |1>.
∴ Z|1> = |0>.
As a summary,
Z|0> = 0, Z|1> = |0>, Z†|0> = |1>, Z†|1> = 0.
The above explanations are about quantum state.
Now I start explaining my theory about quantum history.
A function which represents a classical history.
ν: R → {0,1}.
ν(t) = 0 or 1.
A basis of the quantum history vector space: |ν>.
A quantum history vector: ∫Dν Φ[ν] |ν>.
An operator which acts on a specific time: Z†(t)Z(t)|ν> = ν(t)|ν>.
Uda Equation:
i
∴ i
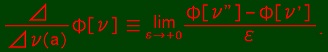
ν'(t) = ν''(t) = ν(t) if t < a or t > a + ε.
ν'(t) = 0 and ν''(t) = 1 if a ≦ t ≦ a + ε.
Uda equation:
-i

Another formulation can stand as follows.
At first, I put a condition [Z(t), Z†(t')]+ = δ(t - t'), [Z(t), Z(t')]+ = 0.
This condition realizes that [Z†(t)Z(t), Z†(t')Z(t')]- = 0.
Then I replace
limε→+0 (1/ε)∫Dν {Φ[ν(□ - ε)] - Φ[ν]} |ν>
with
∫-∞∞dt Z†(t)(d/dt)Z(t)∫Dν Φ[ν] |ν>.
Uda equation:
i
I removed factor α heuristically by seeing dimensionality.
Below I explain what ∫-∞∞dt Z†(t)(d/dt)Z(t) |Φ> means.
∫-∞∞dt Z†(t)(d/dt)Z(t) |Φ>
= limε→0 (1/ε)∫-∞∞dt Z†(t)[Z(t + ε) - Z(t)] |Φ>
= limε→0 (1/ε)∫-∞∞dt [Z†(t - ε) - Z†(t)]Z(t) |Φ>
Z†(t - ε)Z(t) creates a particle at time t - ε after annihilating a particle at time t only if there is a particle at time t.
Z†(t)Z(t) creates a particle at time t after annihilating a particle at time t only if there is a particle at time t.
So, limε→0 (1/ε) [Z†(t - ε) - Z†(t)]Z(t) |Φ> is a kind of partial differentiation only if there is a particle at time t.
limε→0 (1/ε) [Z†(t - ε) - Z†(t)]Z(t) |Φ> = 0 if there is no particle at time t.
As for partial differentiation, the following formula holds.
limε→0 (1/ε) [F(x1 +ε, ・・・, xn + ε) - F(x1, ・・・, xn)]
= Σk=1n limε→0 (1/ε) [F(x1, ・・・, xk-1, xk + ε, xk+1, ・・・, xn) - F(x1, ・・・, xn)]
On the analogy of this, the variation of |Φ> caused by shifting all times when there is a particle by -ε is thought to be
ε∫-∞∞dt Z†(t)(d/dt)Z(t) |Φ>
as ε → 0.
If a quantum history is not entangled in time-like direction at all, to shift all times when there is a particle by -ε is to replace quantum state at time t with quantum state at time t + ε for all t.
This is the very concept of left hand side of Uda equation.